Reason is not without distinction

What faculties allow distinction? Descartes says if 2 + 2 = 4, then not only does 3 + 1 = 4, but these facts imply one another. But to say

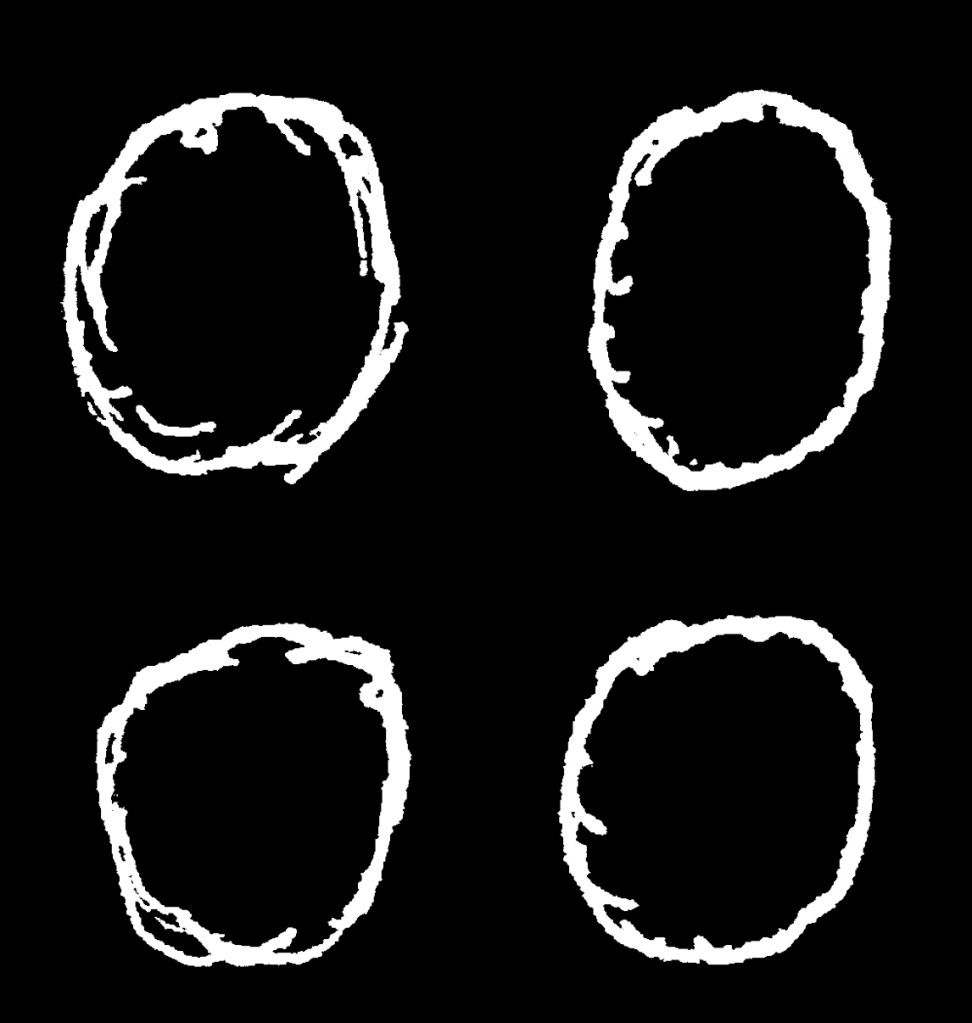
is to say we call “one”, 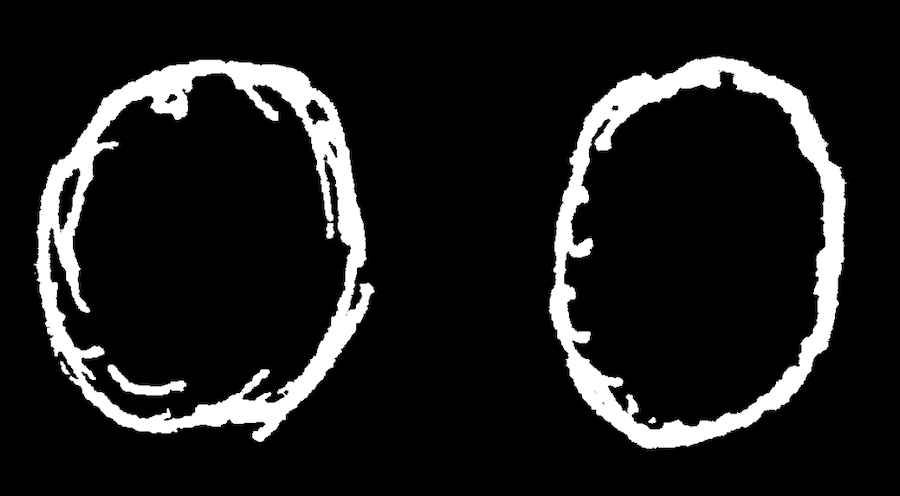“two”, and so on –– but who is to say we draw the line at the line? Is the line not on a plane (perhaps different-colored paper), and is the plane as ideal as the line, something crafted by the human hand? And if I were to tell you “2 + 2 = 4”, you’d suppose I meant

or

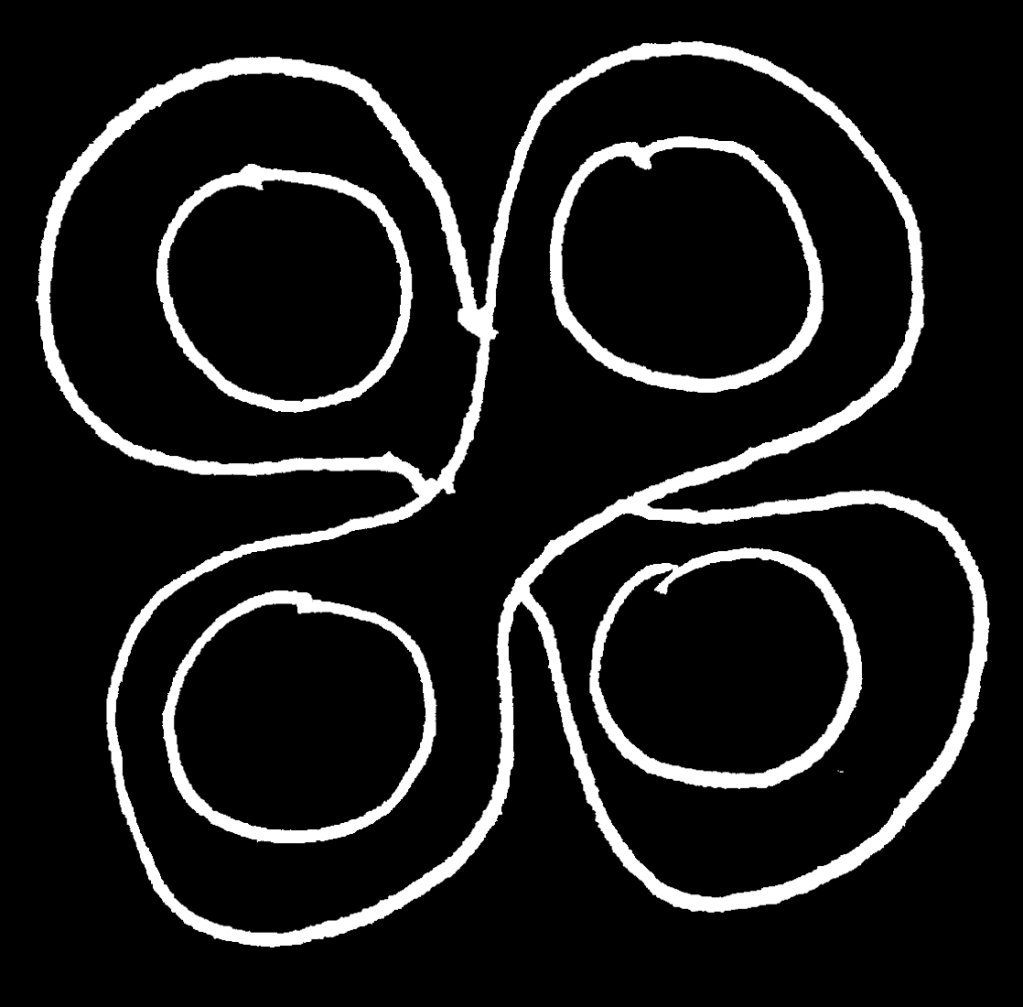
and “3 + 1 = 4” to mean

or

meaning we’d called our circles 1, 2, 3, and 4, in some variation or another.

But who ever was to say succession was allowed –– that counting shall be a labeling of distinct entities whence the mechanism of distinction is yet unknown? Knowledge of “this” or “that” has always foregone debating the business of “this” and “that”. Where does the knowledge of these great intuitions, which permit the mind of man to toil all its life, come from?